Geometry
Over the years I have developed a variety of techniques in the search for new models, such as cutting up (mentally) a known model and joining the ends in new ways. One technique has proved especially useful and deserves to be described here.
Many of my models can be grouped into families of five in which the same basic pattern is expressed in different symmetries. In some cases these relationships are quite obvious, in other cases not so obvious – sometimes even surprising. The implication is that each idea leading to a fascinating new model, at the same time leads to its four cousins that may be just as fascinating. An easy way to construct these four cousins is therefor essential.
The symmetries represented in each family are based on the five platonic solids.

The five solids represent only three symmetry groups, however, each group being expressed in two different ways by pairs of solids called dual pairs: icosahedron-dodecahedron, octahedron-cube and tetrahedron-tetrahedron (the tetrahedron being self-dual).
The task now is to identify the region of a model that corresponds to one rhombic face, then sketch a square diagram illustrating how the strands of the model weave over and under one another within that region. Applying this diagram to the faces of the cube, taking care that like corners meet, yields a schematic model of the first member of the family. Then you stretch the square diagram to fit the faces of the rhombic dodecahedron and copy it to all twelve faces. Since the streching can be done in one of two directions this yields the next two members of the family. The last two members are of course produced by further stretching and application to the faces of the rhombic triacontahedron:
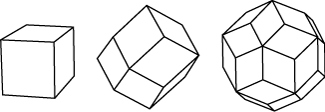
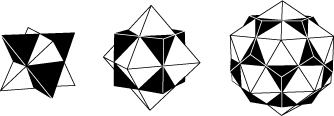
This is elegantly illustrated by these three compounds in which the dual pairs are arranged so that their edges cross one another perpendicularly at their midpoints. Each such pair of crossing edges span a rhomb in which they are the diagonals. In other words the three compounds can be wrapped in the rhombic polyhedra known as the cube, the rhombic dodecahedron and the rhombic triacontahedron.
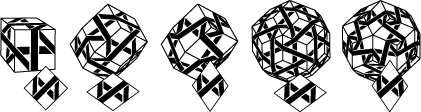
The example used here corresponds to Triple Whitehead, Wave packet, Tetracoil, Halo and Hexacoil, i.e. the top row of in the gallery but in a different order.
Some models give diagrams so simple that they only lead to three different family members, since stretching the diagram one way or the other makes no difference:
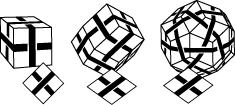
Actually it would make a little difference in this case: it would turn each model into its mirror image. Almost all my models could be made in two mirror equivalent versions, but of course I would not really consider them different models. The example used here corresponds to earlier works that will be included in a later version of this site.